题目分析
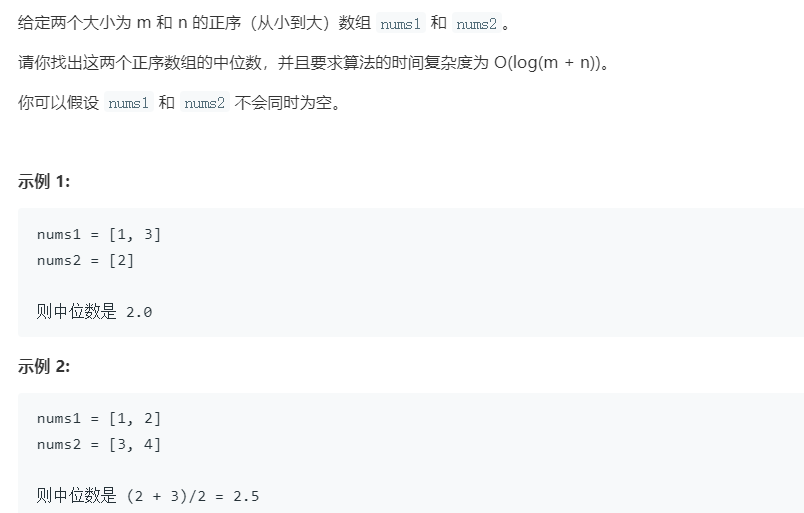
寻找两个正序数组的中位数,这道题本身并不难,但是如何使用O(log(m + n))的时间复杂度求解是这道题目的难点。
合并数组
合并有序数组的方法是最容易想到的方法,在归并排序中就用到了这种思想,将两个有序的数组合并为一个,然后直接索引寻找中位数,时间复杂度为$O(m+n)$,空间复杂度为$O(m+n)$。
1 | class Solution: |
双指针
因为不需要其他的数据,因此我们不需要引入一个新数组保存所有数据,只需要记录当前索引即。时间复杂度为$O(m+n)$,空间复杂度为$O(1)$。
1 | class Solution: |
中位数算法
这道题还有更优的算法,利用中位数的性质和二分查找的思想,将两个数组分成左右两个部分,这种方法参考windliang在Leetcode题解中的思想。时间复杂度为$O(log(min(m+n)))$,空间复杂度为$O(1)$。
1 | class Solution: |
刷题总结
后面跟两种方法,我也是参考别人的题解,不仅思路清晰,而且代码简单,可以说膜拜了。这道题的难点在于二分法的应用,小伙伴们要多刷题,多见一见世面,比较不同算法之间的区别,增强自己的Coding能力。